Método da Bissecção
Zero de função
Método da Bissecção
É um método numérico utilizado para encontrar raízes de funções contínuas. A ideia é dividir o intervalo em que a raiz se encontra e escolher subintervalos em que a função muda de sinal, garantindo que uma raiz exista dentro de cada subintervalo. O processo é repetido até que a precisão desejada seja alcançada.
Fórmula do \( x_k \)
A cada iteração \( k \), o ponto \( x_k \) é calculado como a média dos extremos do intervalo atual: \[ x_k = \frac{a_k + b_k}{2} \] onde \( a_k \) e \( b_k \) são os extremos do intervalo na iteração \( k \).
Fórmula do erro
O erro, ε , em cada iteração é reduzido pela metade, e o erro total
após \( k \) iterações é dado por:
\[ \epsilon_k = b_k - a_k \]
onde \( a_0 \) e \( b_0 \) são os extremos do intervalo inicial.
Número de passos
O número de passos k, necessários para alcançar o erro,
ε , desejado pode ser estimado pela fórmula:
\[ k \geq \frac{\log(b_0 - a_0)-log(\epsilon)}{\log 2} \]
onde \( \epsilon \) é o erro tolerável e k = 0, 1, 2,...,n
Tabela do método
Geralmente o método é apresentado por meio de uma tabela, onde temos os valores de
k, a, sinal de f(a), s(f(a)) , b,
sinal de f(b), s(f(b)) , xk, sinal de f(xk), s(f(xk) e
ε. Da seguinte forma (ou similar):
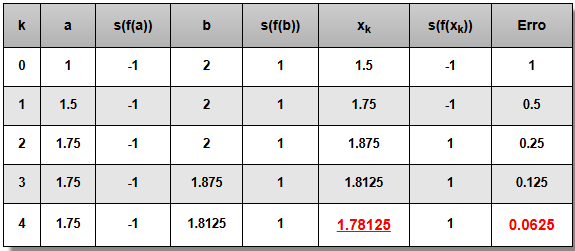
Onde temos: A função, \( f(x) = x.ln(x)-1 \), o intervalo, \([a , b] = [1 , 2] \), o erro, \( \epsilon \leq 0.1 \) e a função sinal \( s(f(x)) \)
Atenção: Na função sinal tesmos: i) se f(x) é postivo: s(f(x)) = 1, e, ii)
se f(x) é negativo: s(f(x)) = -1.
Lembre-se: Neste método s(f(a)) e s(f(b)) devem ter sinais trocados.
Esse método garante que, ao final das iterações, o valor calculado para a raiz está dentro do erro desejado.