Método de Lagrange
Interpolação Polinomial
A interpolação de Lagrange é uma técnica utilizada para encontrar um polinômio de grau \(n-1\) que passe exatamente por um conjunto de pontos dados. Ela é especialmente útil quando você deseja construir o polinômio sem resolver um sistema de equações lineares, ao contrário de outros métodos.
Fórmula do polinômio de Lagrange
Dado um conjunto de \(n\) pontos \( (x_1, y_1), (x_2, y_2), \dots, (x_n, y_n) \), o polinômio de interpolação de Lagrange é dado por:
$$ P_n(x) = \sum_{i=1}^{n} y_i \cdot L_i(x) $$
$$ P_n(x) = y_1 \cdot L_1(x) + y_2 \cdot L_2(x) + ... + y_n \cdot L_n(x) $$
Onde:
- yi são os valores da função nos pontos \( (x_i, y_i) \).
- Li(x) são os polinômios base de Lagrange, definidos como:
$$ L_i(x) = \prod_{\substack{1 \leq j \leq n \\ j \neq i}} \frac{x - x_j}{x_i - x_j} $$
Esses polinômios \( L_i(x) \) têm a propriedade de serem iguais a 1 no ponto \( x_i \) e 0 nos outros pontos \( x_j \) (\( j \neq i \)). Isso permite que o polinômio de interpolação passe exatamente por todos os pontos fornecidos.
Passos para calcular a interpolação de Lagrange:
Calcular os polinômios base \( L_i(x) \): Para cada ponto \( (x_i, y_i) \), calcule o polinômio base \( L_i(x) \) usando a fórmula acima.
Construir o polinômio \( P(x) \): O polinômio de interpolação é a soma dos produtos \( y_i \cdot L_i(x) \) para todos os \( i \), ou seja, o valor \( y_i \) de cada ponto é multiplicado pelo polinômio base correspondente.
Exemplo de interpolação de Lagrange:
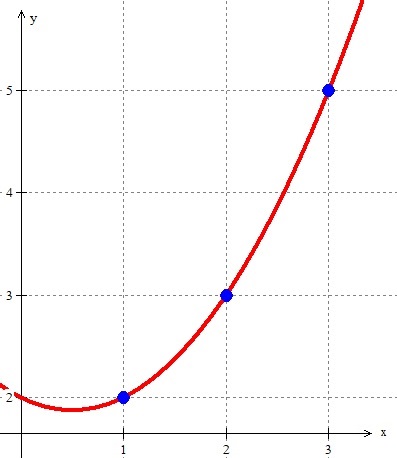
Vamos supor que temos três pontos \( (1, 2), (2, 3), (3, 5) \). O polinômio de interpolação de Lagrange será:
$$ P_2(x) = y_1 \cdot L_1(x) + y_2 \cdot L_2(x) + y_3 \cdot L_3(x) $$
Calculando os polinômios base \( L_1(x), L_2(x), L_3(x) \):
L1(x) = \( \frac{(x - 2)(x - 3)}{(1 - 2)(1 - 3)} = \frac{(x - 2)(x - 3)}{2} \)
L2(x) = \( \frac{(x - 1)(x - 3)}{(2 - 1)(2 - 3)} = -(x - 1)(x - 3) \)
L3(x) = \( \frac{(x - 1)(x - 2)}{(3 - 1)(3 - 2)} = \frac{(x - 1)(x - 2)}{2} \)
Portanto, o polinômio de interpolação será:
$$ P_2(x) = 2 \cdot \frac{(x - 2)(x - 3)}{2} + 3 \cdot -(x - 1)(x - 3) + 5 \cdot \frac{(x - 1)(x - 2)}{2} $$ $$ P_2(x) = 0,5x^2-0,5x+2 $$