O ajuste/regressão , é um problema comum em experimentos científicos, onde devemos obter uma relação matemática c(x) = y , onde c(x) é a curva - funçao matemática - entre duas variáveis "x" e "y" , isto é, obter uma curva que se ajuste aos pontos correspondentes a um conjunto de dados obtidos experimentalmente:

(x1, y1), (x2, y2), ..., (xn, yn)

De modo geral, temos alguma razão teórica para acreditar que estes pontos pertencem a uma mesma reta, parábola ou outro gráfico de função. Na prática, como os dados são obtidos experimentalmente, temos alguns erros de medição, o que torna impossível encontrarmos uma curva que se ajuste perfeitamente a todos os pontos os valores representados por uma máquina (calculadora ou computador, por exemplo) estão suscetíveis a erros.

Veja um exemplo de regressão quadrática na imagem a seguir:

---

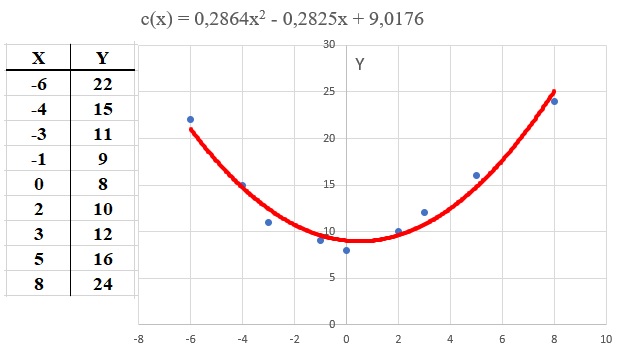
Atenção: O ajuste de curvas ou regressão é uma técnica estatística usada para modelar a relação entre variáveis. O objetivo é encontrar a melhor curva que se ajusta a um conjunto de dados, de forma que possamos fazer previsões ou entender o comportamento de uma variável em função de outra.

A escolha do tipo de ajuste de curva depende do comportamento observado nos dados. Se os dados parecem seguir uma linha reta, a regressão linear é a melhor escolha; se há uma curva, a regressão quadrática pode ser mais adequada; para crescimento ou decaimento exponencial, utiliza-se a regressão exponencial, e assim por diante.

Após aplicar o modelo de regressão, a qualidade do ajuste pode ser medida usando o coeficiente de determinação, R², que indica o quão bem o modelo se ajusta aos dados observados.

---

Voltar à página anterior para escolher outro método de interpolação